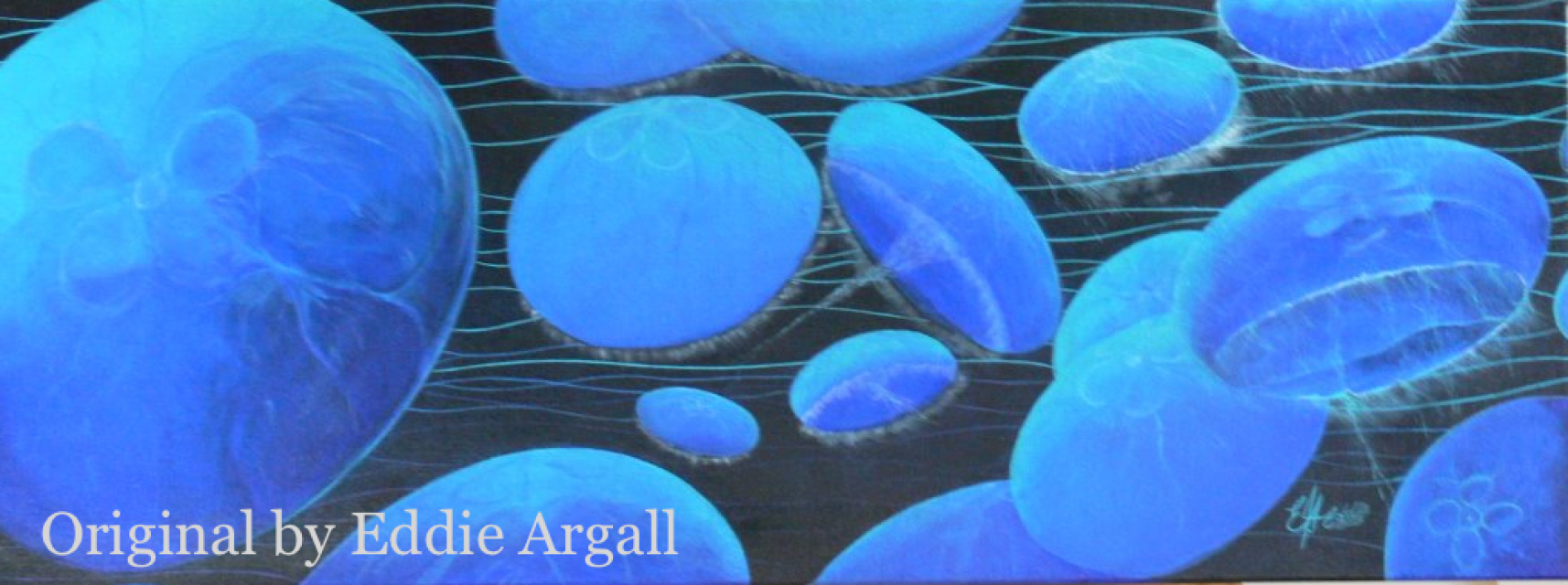
"Jellies"
A$695.00
A$695.00

"Sunrise Reflections"
A$795.00
A$795.00

"Reef Movement"
A$450.00
A$450.00

"Wongaling Beach to Dunk"
A$450.00
A$450.00

"Windy Palm"
A$450.00
A$450.00

"Reef Magic"
A$495.00
A$495.00

"Sunrise Wongaling Beach to Dunk"
A$3,000.00
A$3,000.00

"Sunrise Bliss"
A$695.00
A$695.00

"Palm Cockatoo's" Medium Framed
A$995.00
A$995.00

"Sunset Hue to Dunk "
A$695.00
A$695.00

"Nth Qld Tree Frog" Medium Framed
A$1,795.00
A$1,795.00

"Mission Palms"
A$695.00
A$695.00

"Agave"
A$495.00
A$495.00

"Ulysses"
A$1,995.00
A$1,995.00

"Red Frangipani"
A$695.00
A$695.00

"Banfield Tropics"
A$595.00
A$595.00

"Bromeliad with Lizard""
A$695.00
A$695.00

"Dawn Raider"
A$595.00
A$595.00

"Cassowary Licuala"
A$4,000.00
A$4,000.00

"Turquoise Reef Movement"
A$450.00
A$450.00

"Sea Turtle off Dunk"
A$595.00
A$595.00

"Beach Shack"
A$295.00
A$295.00

"Emu the Forgotten Emblem" Medium Framed
A$995.00
A$995.00

"Tranquillity"
A$595.00
A$595.00

"Tropical Storm"
A$995.00
A$995.00

"Sunset Scatter"
A$495.00
A$495.00

"Roo"
A$3,000.00
A$3,000.00

"Roo"
A$95.00
A$95.00

"Nth Qld Tree Frog"
A$75.00
A$75.00

"Ulysses"
A$75.00
A$75.00

"Hidden Treasure"
A$2,500.00
A$2,500.00

"Cassowary Licuala"
A$395.00
A$395.00

"Forgotten Emblem"
A$4,500.00
A$4,500.00

"Bromeliad with Frog"
A$75.00
A$75.00

"Bromeliad with Frog"
A$95.00
A$95.00
